1. 로그(Log) 활용
로그는 점진적인 증가를 표현하는 데 사용할 수 있다.

예시로는 경험치 시스템이 있겠다.
레벨업에 필요한 경험치를 다음과 같이 설정할 수 있다.

코드 예제
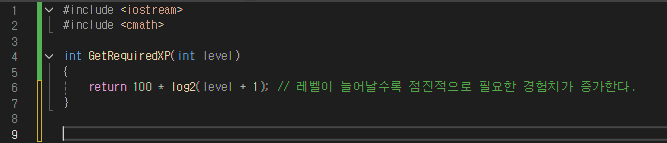
Level 1 인 경우 100xp가 필요하지만
Level 10 인 경우 약 332
Level 50 인 경우 664 가 필요하다
점점 더 많은 경험치를 필요로 하게 만드는 효과가 있다.
2. 지수(Exponential) 활용
지수는 빠르게 증가하는 성장 시스템에 사용할 수 있다.

적 체력 스케일링

레벨이 올라갈수록 체력이 급격히 증가한다.

Level 1 인 경우 100HP 지만
Level 10 인 경우 약 619
Level 50 인 경우 9100이 된다.
로그와 반대로, 급격하게 증가하는 성질을 이용할 수 있다.
3. 시그모이드(Sigmoid) 곡선 : 부드러운 성장
초반에는 완만하게 증가하다가 중간부터 급격히 상승, 이후 다시 느려지는 곡선
사용 예시 : RPG 게임에서 초반에는 레벨업이 빠르고 후반에는 느려지는 시스템

L = 최대값, K = 기울기 조절, x_0 = 중앙값

3. 행렬 연산(Matrix Operations)
3D 게임에서는 행렬(Matrix)을 사용하여 회전, 이동 크기 조정(스케일)을 계산한다.
객체에서 변환을 처리할 때, 일반적으로 4x4 행렬을 사용한다.
각 변환을 행렬로 나타내면 다음과 같아진다.
1. 크기 조정(Scaling) 행렬
크기 조정은 객체의 크기를 변경하는 변환이다. 크기 조정 행렬은 다음과 같다.

여기서 Sx, Sy, Sz는 각축 (x,y,z)에 대한 크기 조정 비율이다.
스케일을 2배로 확대한다면

이런식으로 된다.
2. 이동(Translation) 행렬
이동은 객체를 특정 방향으로 움직이는 변환입니다. 이동 행렬은 다음과 같다.

여기서 Tx, Ty, Tz는 각각 x,y,z축으로의 이동 거리이다.
만약 3,5,-1 만큼 이동하는 행렬로 표현하면

이런식으로 표현이 가능하다.
3. 회전(Rotation) 행렬
회전 변환은 x,y,z축을 기준으로 회전할 수 있다.
각 축을 기준으로 회전하는 행렬은 다음과 같습니다.
X축 회전(Roll)

Y축 회전(Pitch)

Z축 회전(Yaw)

Z축을 90도 회전한다면 삼각함수에 따라
sin 90 = 1
cos 90 = 0 으로 표현되어

이런식의 행렬이 된다.
4. 변환 행렬을 이용한 변환 연산
객체의 좌표를 변환 행렬과 곱하면 변환된 좌표를 얻을 수 있습니다.
1. 좌표 변환 공식
어떤 점 P = (x,y,z,1)이 있을 때, 변환 행렬 M을 적용하면 새로운 좌표 P'를 얻는다.

5. 복합 변환(Multiple Transformations)
게임에서는 이동 + 회전 + 크기 조정을 조합하여 적용한다.
순서가 중요하며, 보통 크기 조정 -> 회전 -> 이동 순으로 수행된다.
T * R * S 로 표현된다.
예시로 크기 조정(2,2,2) -> Y축 30도 회전 -> (3,4,5)로 이동한다고 하면
M = T(3,4,5) * Ry(30도) x S(2,2,2) 가 된다.
계산을 해보자
1. 크기 조정(Scaling) 행렬
2,2,2 크기

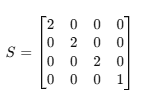
2. Y 축 회전(Rotation Y) 행렬
Y축 30도 회전
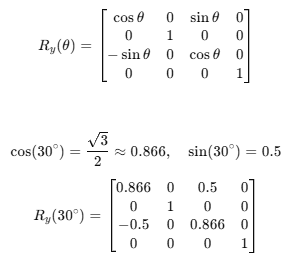
3. 이동(Translation) 행렬
3,4,5 로 이동

각 행렬을 구했으면 행렬의 곱을 수행하여 값을 구해준다.
T * ( R * S) 로
R 과 S의 계산 먼저 수행해준다.

행렬의 곱은 아래의 사진 처럼 같은 색끼리 곱해지며 각 항마다 값을 구해준다.

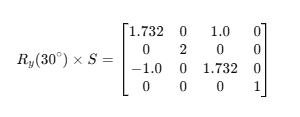
해당 과정을 수행하면 이러한 행렬이 나오게 된다.
다음 구해진 행렬을 T ( 이동 행렬 )와 곱을 해준다.


최종 결과 M은 위의 사진처럼 나오게되고
해당 행렬을 사용하면
객체가 2배의 크기로 조정된 후, Y축을 기준으로 30도 회전, (3,4,5)의 위치로 이동된 최종 좌표를 구할 수 있다.
4. 코드 예제
3D 그래픽스에서 변환을 적용하려면 4x4 행렬(Matritx4x4)를 사용해야 한다.

우선 4차원 벡터 Vector4D를 정의하고
기존 3D벡터에는 w 좌표가 없으므로, 변환을 위해 w = 1을 추가한 4D 벡터를 사용한다.
여기서 w = 1을 주는 이유는
이동 변환(Translation)을 적용할 수 있도록 하기 위함이다.
다음 4차원 벡터를 변환하기 위해서는 4x4 행렬을 사용해야 한다.

이제 행렬을 정의하면 변환이 가능하다
m[3][0], m[3][1], m[3][2] : 이동(T)을 담당
최종 변환후 w != 1 이면 정규화가 필요하다 (x /= w, y /=, z /= w) 로 계산

각각의 값을 행렬로 바꾸어 주고 이제 복합 변환을 적용하여 준다.
행렬의 곱 연산 추가


'Math' 카테고리의 다른 글
| 게임에서 사용하는 수학 활용 공부(3) OBB 충돌 (0) | 2025.03.26 |
|---|---|
| 게임에서 사용하는 수학 활용 공부(2) (0) | 2025.03.25 |
| 삼각함수를 이용한 게임 수학 (1) | 2025.03.24 |
| 행렬의 곱셈 (0) | 2024.12.04 |
| 삼각함수 기초(1) (2) | 2024.01.04 |



