1. 삼각함수
사인 (sin), 코사인 (cos), 탄젠트 (tan)
- 직각삼각형에서 변의 길이 비율을 나타냄
- 원형 운동, 회전 등에 사용된다

1. 라디안 (Radian) : 각도 대신 원주율 기준으로 각을 표현
- 1 radian = 약 57.3도
- 360도 = 2pi rad
2. 피타고라스 정리
- a^2 + b^2 = c^2
- 거리 계산 등에 사용된다.
1. 삼각함수의 덧셈 정리
삼각함수의 덧셈 정리는 두 개의 각을 더하거나 빼는 경우, 해당 삼각함수 값을 어떻게 구할 수 있는지를 나타내는 공식이다.
이 공식은 이미 알고 있는 삼각함수 값들을 조합하여 새로운 값을 빠르게 계산할 수 있도록 도와준다.
1. 코사인과 사인의 덧셈 정리
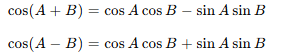
2. 사인의 덧셈 정리

3. 탄젠트의 덧셈 정리

탄젠트는 분수 형태로 표현되며, 분모가 0이 되지 않도록 주의해야 한다.
2. 게임에서의 사용
1. 2D회전
- 캐릭터가 특정 각도로 회전하는 경우를 말한다
2D에서 어떤 점 (x,y)를 원전 (0,0)을 기준으로 θ 만큼 회전하려면 다음 변환식을 사용한다.
X = x Cos θ - y Sin θ
Y = x Sin θ + y Cos θ
(X,Y)는 회전 후 새로운 좌표
θ 는 회전 각도(라디안 단위)
예를 들어 10 Cos(40) - 5 Sin (20) 이라고 하였을 때
40 20 각도로 표시된 값을 라디안 값으로 변환한다.
라디안 값 = 각도 * pi / 180 로 계산이 가능하다
코사인 값을 직접 계산하기 위해서는 테일러 급수(Taylor Series), 유클리드 기하학적 접근, 또는 삼각함수 표를 이용하는 방법이 있다.
1. 테일러 급수를 이용한 근사 계산

여기서 x는 라디안 단위로 변환된 값으로
40도를 라디안으로 변환시키고

그것을 테일러급수 수식에 반영하면 이런식으로 나오게 된다.

몇 개 항을 사용해서 근사를 계산하면

cos 40 0.766에 가까운 값을 얻을 수 있다.
2. 삼각함수의 반복 공식 사용
삼각함수는 기본적인 값을 알고 있으면, 여러 공식을 사용하여 구할 수 있다.
예를 들어, 각도의 덧셈 정리를 이용하면
Cos(40) = Cos(30 + 10)으로 나눌 수 있고 삼각함수 덧셈 정리를 사용하여
Cos(A + B) = Cos A cos B - Sin A Sin B 이런식으로 정리가 가능하다
다음 삼각함수 표를 이용하여
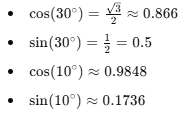
알 수 있는 값은 바로 알아내고 나머지 모르는 값은 테일러 급수를 이용하여 값을 구해준다.
그 다음 위의 해당 식을 이용하면

해당 0.766을 얻을 수 있다.
3. 테일러 급수와 삼각함수 공식 비교
1. 테일러 급수
테일러 급수를 사용하면 삼각함수 값을 이론적으로 정확하게 계산할 수 있다.
하지만 테일러 급수는 많은 항을 계산해야 할수록 정확도가 올라가고, 연산량이 많아지는 문제점이 있다.
예를 들어 Cos(10)을 계산할 경우 테일러 급수의 첫 3~4개 항만 사용해도 꽤 근사한 값을 얻을 수 있다.
하지만 0.1도 값은 아주 작은 각도에서는 더 많은 항이 필요하고 부동소수점 연산이 많이 필요해 느려질 수 있다.
그렇기에 테일러 급수는 이론적으로 정확하지만, 직접 계산하려면 많은 연산이 필요하여 효율성이 떨어질 수 있다.
2. 삼각 함수 공식
삼각함수 공식(덧셈, 뺄셈)을 사용하면, 이미 알고 있는 값들을 조합해 새로운 값을 빠르게 계산할 수 있는 장점이 있다.
덧셈 정리를 사용한다고 하면
Cos(40) = Cos(30 + 10) , Cos(30) * Cos(10) - Sin(30) * Sin(10)
이렇게 하면 30도 같은 경우는 이미 알려진 값들을 활용해 새로운 값을 빠르게 구할 수 있다.
이 과정을 사용하면 테일러 급수를 직접 계산하는 것보다 적은 연산으로 값을 구할 수 있게 된다.
3. 컴퓨터의 계산 방식
컴퓨터는 테일러 급수를 직접 사용하기 보다는 알고리즘(CORDIC, 룩업 테이블 등)을 활용해 계산한다.
이러한 알고리즘은 삼각함수의 여러 공식을 사용해 반복적인 곱셈/덧셈 연산만으로 빠르게 값을 구하는 방식을 이용한다.
그러면 다시 원점으로 돌아와 해당 2D회전에 대한 값은 이러한 삼각함수의 공식을 이용하여 좌표값을 구할 수 있다.
4. 코드 구현
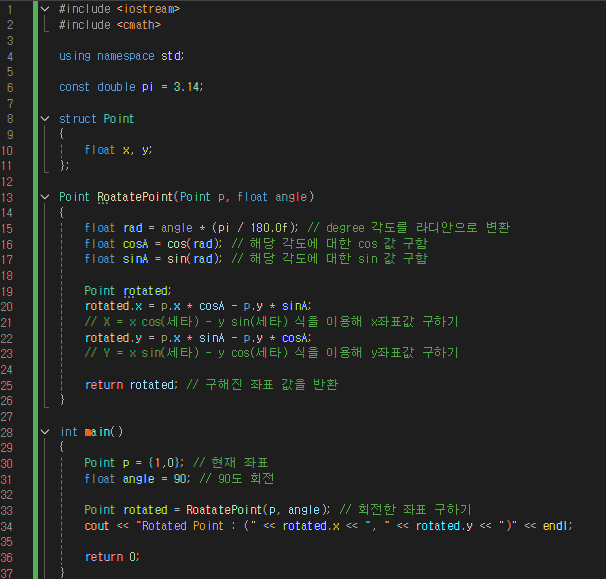
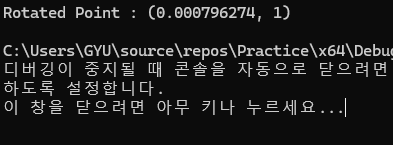
2. 3D 회전
3D 에서는 X,Y,Z 축을 중심으로 개별적으로 회전이 가능하다.
각 축을 기준으로 회전하는 행렬 변환식은 다음과 같다.
X축 회전(Pitch)
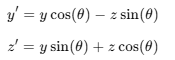
Y축 회전 (Yaw)
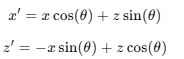
Z축 회전 (Roll)
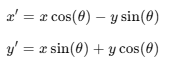
Yaw = 좌우 회전(Y축 기준)
Pitch = 위아래 회전(X축 기준)
Roll = 기울기 회전(Z축 기준)
유니티와 언리얼에서는 Quaternion을 사용하여 회전을 다루는 것이 일반적이다.
3D 회전도 위의 2D와 마찬가지로 각 좌표값을 구해주는 식으로 구할 수 있다.
2. 카메라 시점 회전
게임에서 FPS 또는 3인칭 카메라를 구현할 경우, Yaw(좌우 회전), Pitch(상하 회전)을 조절해야 한다.
FPS 카메라 회전 원리
1. Yaw (Y축 회전)
- 마우스의 좌우 이동(X값 증가 / 감소)에 따라 Yaw(좌우 회전)을 조절
- yaw += mouse X * Sensitivity(마우스 이동);
- yaw 값을 적용할 때 cos(yaw), sin(yaw)를 이용해 방향 벡터를 계산할 수 있다.
2. Pitch (X축 회전)
- 마우스의 상하 이동(Y값 증가 / 감소)에 따라 Pitch(상하 회전)을 조절
- pitch += mouse Y * Sensitivity(마우스 이동);
- pitch는 -90 ~ + 90도 범위로 제한해야 한다.
3. 언리얼 엔진을 이용한 FPS 카메라 회전 코드

LookUp(float value) : 마우스 위아래 움직임 -> Pitch 값 조절
Turn(float value) : 마우스 좌우 움직임 -> Yaw 값 조절
FMath::Clamp() 함수 이용하여 Pitch가 -90 ~ 90도를 초과하지 못하게 제한
3. 포물선 운동(Projectile Motion)
게임에서 총알, 화살, 투사체 궤적을 구현할 경우 중력 영향을 받는 포물선 운동을 적용하여야 한다.
1. 포물선 운동의 공식
x = v' Cos(θ) * t
y = v' Sin(θ) * t - 1/2 * gt^2;
v' = 초기 속도
θ = 발사 각도
g = 중력 가속도 ( 일반적으로 9.81 m/s^2)
t = 경과 시간
2. 코드 예제
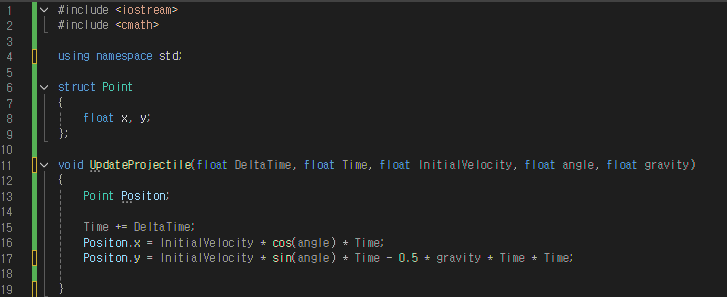
게임 에서는 활을 쏠대 angle 값을 조절하여 높이와 도달 거리에 변화를 주고
총알 궤적에서 Gravity를 조절해 현실적인 탄도 구현이 가능하다.
4. 특정 방향 바라보기
게임에서 캐릭터가 목표 지점을 바라보게 만들기 위해서는 목표 위치로 향하는 각도를 구해야 한다.
1. 목표 지점 방향 구하는 공식
θ(목표 각도) = atan2 ( targetY(목표y 좌표) - CurrentY(현재 Y좌표), TargetX(목표x 좌표) - CurrentX(현재 x좌표)
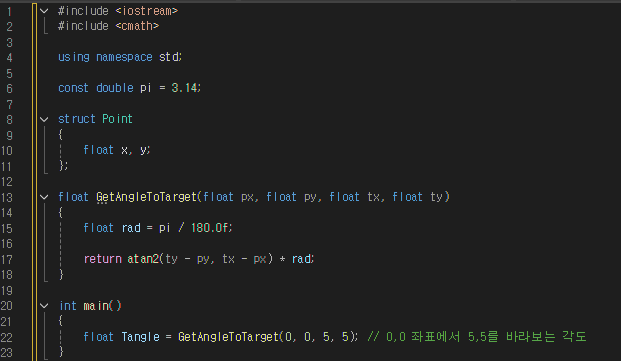
2. atan 계산 방법
atan은 주어진 값 x에 대해 각도를 구하는 함수이다.
일반적인 삼각함수 처럼 간단한 공식으로 직접 계산은 불가능하여, 여러 방법을 활용해야 한다.
1. 테일러 급수 이용
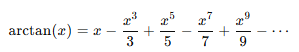
이 급수는 절대갑 x <= 1 일 때 빠르게 수렴하며 > 인 경우 수렴이 느려 다른 변환이 필요하다.
atan(0.5)를 계산하면
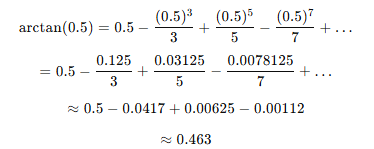
이런식으로 표현 가능
> 인경우에는 atan의 성질을 이용한 변환을 사용해 푸는것이 좋다.
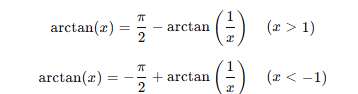
atan(2)인 경우를 계산
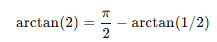
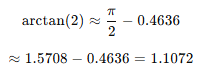
컴퓨터에서는 일반적으로 CORDIC 알고리즘을 사용하여 빠르게 계산한다.
이 방법은 테이블을 미리 만들어 회전 변환을 반복하여 근사값을 빠르게 구하는 방식이다.
5. 유닛 벡터와 방향 벡터
게임 에서 이동 방향을 설정하거나 AI가 특정 방향으로 움직이게 하려면 유닛 벡터가 필요하다.
1. 유닛 벡터
normalization 벡터의 정규화라고 불린다.
길이가 1인 벡터를 말한다. 즉 벡터의 크기가 1인 벡터를 의미하며 주로 방향을 나타내는데에 사용할 수 있다.
1. 벡터의 크기(Magnitude)
먼저 벡터의 크기를 계산하는 방법,
2차원 벡터 v = (x,y)의 크기는 다음과 같이 계산한다.
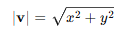
3차원 벡터는
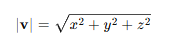
이런식으로 표현하며, 벡터의 크기가 1이면 그 벡터는 유닛 벡터라고 부를 수 있다.
2. 유닛 벡터의 정의
유닛 벡터는 길이가 1인 벡터를 의미한다. 즉 유닛 벡터 u는 다음과 같은 특성을 가진다.
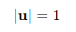
벡터 v가 있을 때, v를 유닛 벡터로 변환하려면 v를 v의 크기로 나누면 된다.
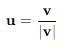
이렇게 하면 u는 v와 같은 방향을 가지며, 크기가 1인 벡터가 된다.
3. 유닛 벡터의 예시
1. 2D 예시
벡터 v = (3,4)라고 하였을때, 해당 벡터의 크기를 구하면
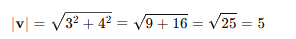
이 벡터를 유닛 벡터로 변환 하려면 v를 5로 나누면 된다.
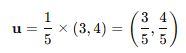
따라서, 유닛 벡터 u = (3/5, 4/5)로 크기가 1인 벡터가 된다.
2. 3D 예시
벡터 v = (1,2,2)라고 했을때
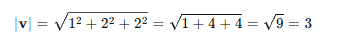
유닛 벡터로 변환하면
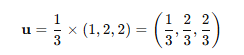
유닛 벡터 u = (1/3, 2/3, 2/3)으로 크기가 1인 벡터가 된다.
4. 유닛 벡터의 용도
유닛 벡터는 주로 방향을 표현할 때 사용된다. 예를 들어 3D 그래픽스나 물리학에서는 물체의 이동 방향이나
힘의 방향을 나타낼 때 유닛 벡터를 사용한다.
5. 코드구현 예제
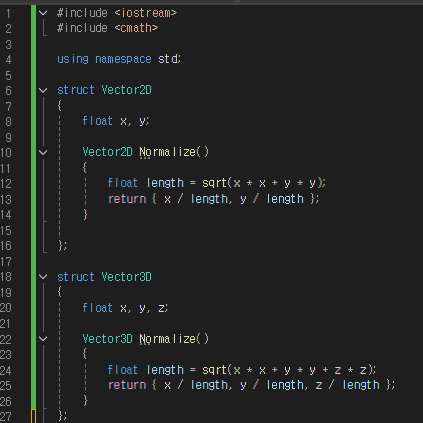
캐릭터가 특정 방향으로 일정 속도로 이동할 때 Normalize()를 사용하면 된다.
AI가 목표 지점을 따라가려면 방향 벡터를 유닛 벡터로 변환해서 사용한다.
6. 내적(Dot Product)과 두 벡터 사이의 각도
두 개의 벡터가 이루는 각도를 구하거나, 두 벡터가 얼마나 유사한 방향인지 비교할 경우에 사용한다.
두 벡터 A, B의 내적 공식은
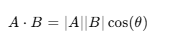
해당 공식을 변형하면 두 벡터 사이의 각도를 구할 수 있다.
|A| 와 |B| 는 A와 B의 크기를 나타내고
θ는 두 벡터 A와 B 사이의 각도를 나타낸다.
두 벡터 A(3,4) 와 B(2,1) 이라고 했을때 A와 B의 내적을 구해보겠다.
1. 벡터 크기 계산
우선 각 A와 B의 크기를 계산해 준다.
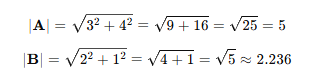
2. cos 각도 구하는 방법
현재 Cos θ 의 값을 모르기에
해당 값을 먼저 구해본다.
내적 A*B 의 값은 = (3 * 2) + (4 * 1)로 계산이 가능하며 값은 10이다.
내적 공식을 활용하면 cos의 값은
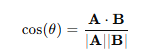
이런식으로 표현이 가능하며
cos = 10 / 5 * 2.236 으로
0.894가 된다.
따라서 θ의 값은 acos(0.894)로 약 26.57도가 나온다
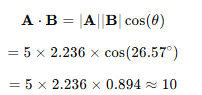
이 값을 이용하면 내적의 값도 약 10이 나오는 것을 확인할 수 있다.
3. 코드 구현
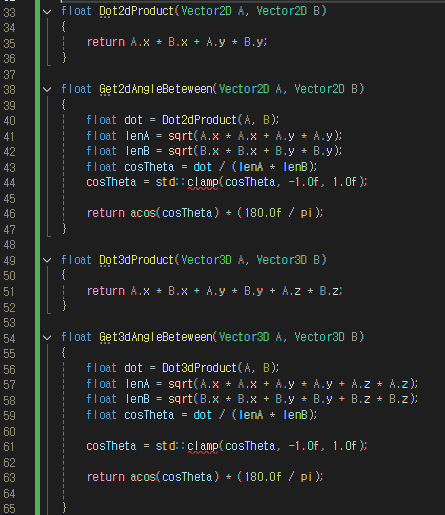
시야(FOV, Field of view)체크 : AI가 플레이어를 볼 수 있는지 판별
두 캐릭터의 시선 방향 비교 : 적이 플레이어를 볼 수 있는지 체크할 때 사용
3D 에서는 Z축을 포함하여 계산
A = (3,4,0) B = (2,1,0)이라고 했을때
1. 내적
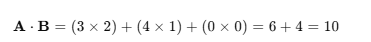
2. 벡터의 크기
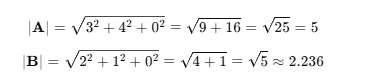
3. 각도 계산
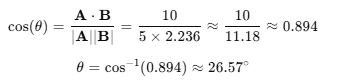
이렇게 구할 수 있다. 코드는 위에 2d와 같이 올렸다.
7. 외적(Cross Product)과 3D 회전 방향
3D에서 두 벡터가 이루는 수직 방향 벡터를 구할 경우 사용
3D 게임 에서는 정확한 회전 방향을 결정하는 데 필요하다.
1. 3D 벡터의 외적 공식
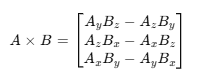
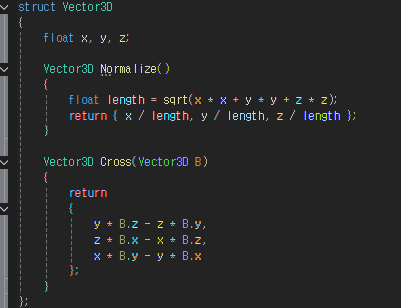
카메라 회전 : 외적을 사용해 새로운 오른쪽 벡터를 구할 수 있음
3D 물리 엔진 : 힘의 토크 계산 시 사용 가능
8. 삼각함수를 활용한 부드러운 회전 (LERP & SLERP)
캐릭터가 부자연스럽게 각도를 바꾸지 않고 부드럽게 회전하게 만들고 싶다면
LERP(선형 보간) 또는 SLERP(구면 선형 보간)을 사용한다.
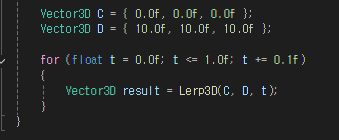
1. 선형 보간(LERP)
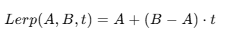
A : 시작 값
B : 목표 값
t = 0 ~1사이의 값( 0이면 A, 1이면 B)
만약 A = 3,4,0 이고 B = 6,8,0 , t = 0.5(보간 진행률 : 이동에 시간 따라 달라짐)
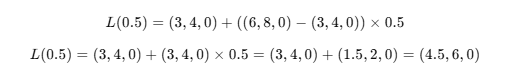
t = 0.5인경우 공식에 따라 보간 값은 (4.5, 6, 0)이 된다.
즉 t 는 보간 계수(Interpolation factor) 라고 불리며, 선형 보간에서 현재 위치를 결정하는 중요한 값이다.
t 는 0과 1사이의 값으로, 보간을 수행하는 두 점 사이에 진행 정도를 나타낸다.
0이면 시작값 A 즉, 보간이 시작된 지점
1이면 목표값 B로 보간이 끝나는 지점이다.
t는 애니메이션에서는 시간의 흐름에 따라 객체가 이동하는 정도를 나타내고,
게임 프로그래밍에서는 두 위치 간의 선형 보간을 통해 객체의 위치를 자연스럽게 이동시키고
그래픽스 에서는 색상이나 카메라의 위치, 회전 등을 보간하는 데 유용하다.
t를 곱하였을떄 부드럽게 변화하는 이유로는
( B- A) 부분에서 시작 값과 목표 값 사이의 차이이다.
이 차이에 t를 곱하여 시간에 따라 그 차이를 점차적으로 따라가도록 만들어 준다.
직선적으로 t 값을 점차적으로 변화시키면 값은 자연스럽게 A에서 B로 부드럽게 이동하게 된다.
'Math' 카테고리의 다른 글
| 게임에서 사용하는 수학 활용 공부(3) OBB 충돌 (0) | 2025.03.26 |
|---|---|
| 게임에서 사용하는 수학 활용 공부(2) (0) | 2025.03.25 |
| 게임에서 사용하는 수학 활용 공부(1) (0) | 2025.03.25 |
| 행렬의 곱셈 (0) | 2024.12.04 |
| 삼각함수 기초(1) (2) | 2024.01.04 |



