Gimbal Lock, Quaternion

짐벌락이란 오일러각(x,y,z)을 이용한 회전 과정에서 두개 혹은 세개의 축이 겹치게되어, 한개 혹은 두개의 축이 자유도를 잃어 같은 방향으로 Objecter의 회전 축이 겹치는 현상으로 겹친 축을 원하는 방향으로 회전 할 수 없는 상태이다.
우선 컴퓨터에서 축을 돌리는 경우를 생각을 해보자 3개의 물체를 동일한 각도로 xyz축을 순서만 다르게 하여 계산을 하면 3개의 물체가 각각 다른 방향을 나타나게 된다. 그렇기에 원하는 회전을 할려면 순서가 필요하다, 그 순서를 계층 구조로 만들어 x-y-z로 임의로 설정을 해주고 돌려주게 된다.
짐벌락이 생기는 이유로는 위의 내용을 설정을 해준다음 돌려주게 되면, 순서에대한 계층 관계에 따라 x를 움직일경우 y축과 같이 y를 움직이면 z축과 같이 z를 돌릴경우에는 단독으로 움직이게 된다. 이러한 상태로 xyz를 돌리다보면 y를 움직였을 경우에 x와 z의 회전축이 겹치게 되면서 짐벌락이 생기게 된다.
그러면 쿼터니언이 어떻게 짐벌락을 피할 수 있는가?
우선 쿼터니언에 대해 자세히 알아야 한다.
쿼터니언이란 3D 그래픽에서 회전을 표현할 때, 행렬 대신 사용하는 수학적 개념으로 4개의 값으로 이루어진 복소수(Complex Number)체계이다.
쿼터니언은 4차원 복소수 공간의 벡터로서 다음과 같이 나타낸다.
q = <w,x,y,z> = w + xi + yi + zk
- 쿼터니언을 q = s + v 형태로 쓰기도 하는데, 여기서 s = q의 w의 스칼라(Scalar) 값이고, v = q의 x,y,z 성분에 해당하는 벡터 부분이다.

쿼터니언의 곱은 일반적인 분배법칙을 따르며 허수 성분인 i, j, k는 다음과 같은 특징을 갖고

곱셈의 교환법칙이 성립하지 않는다.

같은 두 쿼터니언 q1,q2가 있을 때, 두 쿼터니언의 곱 q1,q2는 다음과 같다.

쿼터니언을 스칼라, 벡터 형태로 표기를 하면 위와 같은 식으로 표현이 되고

두 쿼터니언의 곱은 위와 같이 형성된다.
이는 앞에서 나온 q1과 q2의 곱의 부호를 제외하고 곱을 하였을때 나오는 값과 같다.

쿼터니언은 켤레를 갖는다.


쿼터니언의 역수
- 단위 쿼터니언을 갖는다.
q =[1,(0,0,0)]

단위 쿼터니언은 3D 공간에서 오일러, Axis 대신 방향을 표현한다.
쿼터니언으로 방향을 표현하려면 쿼터니언을 행렬로 변환하거나, 행렬을 쿼터니언으로 변환하는 방법이 필요하다.

사원수의 회전 - 축 A에 대한 각도 세타 만큼의 회전을 사원수로 나타낸 식

최종적으로 얻어진 사원수를 행렬로 변환하면, 위의 그림과 같다.
보간(Interpolation)이란 처음과 끝의 값을 가지고 중간에 이어지는 값을 계산해 내는 것이다.
물체의 애니메이션을 수행할 때, 보간을 통해 계산된 키 프레임 사이의 중간 방향을 생성한다.
가장 간단한 보간은 선형보간(Linear Interpolation)으로 두 개의 값을 점으로 생각하고 두개의 점을 이어주는 선의 방정식으로부터 값을 얻어애는 방법이다.

두 사원수 q1,q2에 대해, 선형 보간된 사원수 q(t)는 위의 그림과 같다.

이러한 사원수는 정규화(Nomalize)를 해주어야 한다. 이 함수 q(t)는 q1과 q2사이의 호를 따라간다.
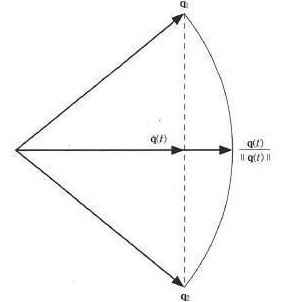
정규화를 할 시 쿼터니언은 4차원 단위 구의 표면을 따라가게 되고,
이런한 선형 보간은 간단하고, 효과적이지만 호를 일정한 비율로 추적을 하지 않는다 그렇기에,
구면 선형 보간(Spherical Linear Interpolation)을 유도하게 되면,

이러한 식이 나오게 된다.
쿼터니언의 특징으로는
1. 짐벌락을 최대한 피할수 있다.
2. 행렬보다 점유 메모리 영역이 작고 부하도 낮다.
3. x,y,z 축에 국한되지 않는 임의의 회전축에서의 회전을 손쉽게 할 수 있다.
4. 회전을 간단히 합성할 수 있고, 오차 또한 쉽게 발생하지 않는다.
5. 두 개 회전사이의 매끄러운 보간을 표현할 수 있다.